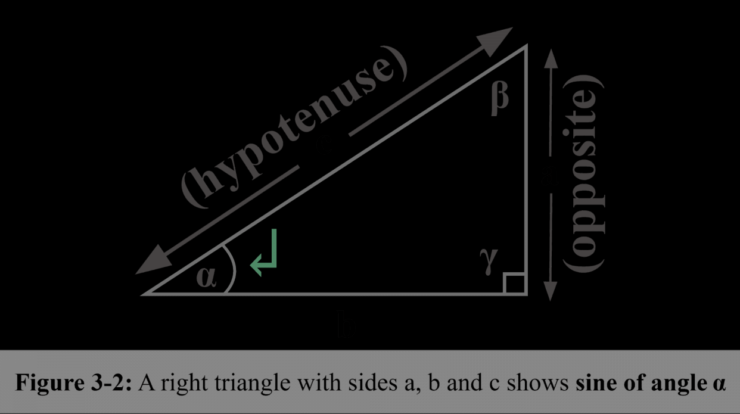
Sine definition – In the realm of trigonometry, the sine function stands as a pivotal concept, defining the ratio of the opposite side to the hypotenuse in a right-angled triangle. Its mathematical properties, graphical representation, and diverse applications across disciplines make it an indispensable tool for problem-solving and understanding the world around us.

Delving into the intricacies of sine, we explore its periodicity, range, and symmetry, revealing its fundamental characteristics. We unravel its relationship with other trigonometric functions, such as cosine and tangent, showcasing their interconnectedness.

Definition and Explanation

The sine function is a trigonometric function that represents the vertical coordinate of a point on a unit circle. It is defined as the ratio of the length of the side opposite an angle in a right triangle to the length of the hypotenuse.

In other words, sine(θ) = opposite/hypotenuse, where θ is the angle opposite the side of length opposite.

Mathematical Properties

• Periodicity: The sine function has a period of 2π, meaning that it repeats itself every 2π units.
• Range: The range of the sine function is [-1, 1].
• Symmetry: The sine function is an odd function, meaning that it is symmetric about the origin.
• Relationship to Other Trigonometric Functions: The sine function is related to other trigonometric functions, such as cosine and tangent, by the following identities:
• sin ²(θ) + cos ²(θ) = 1
• tan(θ) = sin(θ)/cos(θ)

Applications in Trigonometry

The sine function is used to solve trigonometric equations and identities. For example, it can be used to find the value of an angle given the value of its sine.

The sine function is also used in solving real-world problems involving angles and triangles. For example, it can be used to find the height of a building or the distance to a star.

Graphical Representation

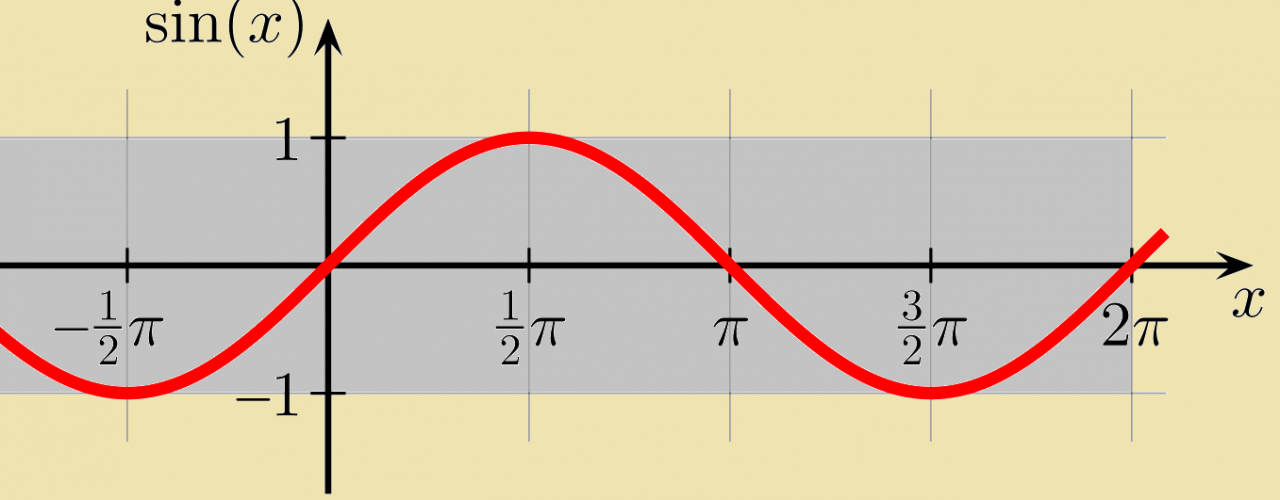
The sine function can be represented graphically as a wave. The amplitude of the wave is 1, the period is 2π, and the phase shift is 0.

The following graph shows the sine function:

Applications in Real-World Scenarios

The sine function is used in various fields, such as engineering, physics, and music.

• In engineering, the sine function is used to analyze the vibrations of structures.
• In physics, the sine function is used to describe the motion of objects in harmonic motion.
• In music, the sine function is used to create sound waves.

Final Summary

From solving trigonometric equations to modeling real-world phenomena, the sine function proves its versatility. In engineering, it aids in analyzing vibrations and oscillations. In physics, it describes wave patterns and acoustic properties. Even in music, it shapes the very essence of sound, determining the pitch and timbre of musical notes.

The sine definition, with its profound implications, stands as a testament to the power of mathematics in unraveling the complexities of our universe.

FAQ Summary: Sine Definition

What is the primary application of sine in trigonometry?

Sine is primarily used to find the ratio of the opposite side to the hypotenuse in a right-angled triangle, which is crucial for solving trigonometric equations and identities.

How is sine related to other trigonometric functions?

Sine is closely related to cosine and tangent. The Pythagorean identity (sin²θ + cos²θ = 1) establishes their interdependence, and the tangent function can be expressed as the ratio of sine to cosine (tanθ = sinθ/cosθ).

What are some real-world examples of sine applications?

Sine finds applications in various fields, including engineering, physics, and music. In engineering, it is used to analyze vibrations and oscillations. In physics, it describes wave patterns and acoustic properties. In music, it determines the pitch and timbre of musical notes.